One of the things that improved a lot in C++11, and even more so in C++17, is the std::algorithm part of the standard library. Its intention is to provide solid implementations of useful algorithms, so developers don’t need to keep reinventing the wheel. Using a built in implementation of an algorithm, one that’s more or less guaranteed to be correct, portable and won’t crash your plugin, does sound very attractive. In addition it reduces code size and generally results in cleaner and clearer code. But how’s the performance?
The reality is that audio processing often has much stricter requirements on performance that what is common for most applications. Ideally the std::algorithm implementations would need to be fast and not allocate memory, use syscalls, excessive redirections, scattered memory access patterns, or anything else that would be detrimental for performance. Ideally they would also be able to utilise parallelisation techniques such as SIMD instructions where possible.
In this blog post we’ll look at a few functions from std::algorithm and compare their performance with manually coded algorithms. We’ll also get under the hood and take a look at how the compiler translates them to machine code.
Digital signal processing on a modern CPU is mostly done using floating point math. One major benefit over integer math is that floating point representations have an almost infinite dynamic range. However at some point the signal needs to be converted down to much more limited range in order to be sent through a Digital to audio converter (DAC) to headphones or speakers. It is a commonly used convention to map the floating point range [-1, 1] to this limited range. Anything outside this range will be truncated, resulting in harsh distortion.
In reality, clip detection is a more complex problem[1], as it’s possible to have intra-sample peaks that are louder than single samples. For this exercise however we can simply assume that finding samples outside of [-1, 1] is enough to detect when a signal is clipping.
std::minmax_element is an algorithm introduced in C++17 that iterates through a collection and finds the smallest and largest values in it. That sounds more or less exactly what we need for clip detection – all we need is to test if the maximum value is > 1, or the minimum value is < -1.
We’ll be using an std::array of floats as a quick stand-in for a single-channel audio buffer populated with random data. We also run the measurements 3 times, with 0, 1% and 50% clipped samples. This is to test whether the algorithm’s performance depends on the data used. Caches and branch prediction could affect the results, so no clipped samples and 50% clipped samples should match the best and worst case respectively for a branch predictor.
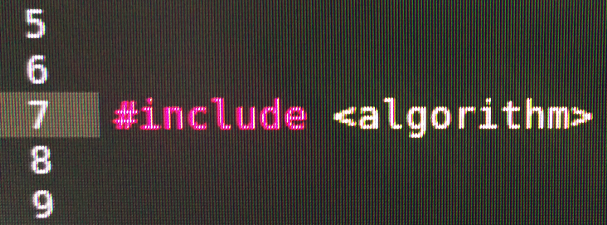
using AudioBuffer = std::array<float, AUDIO_BUFFER_SIZE>;
All the numbers in the article are from our Rocket development board (sporting an Intel Atom X5-Z8350 CPU), with a buffer size of 64 samples. All code is available below, so you are very welcome to run the test yourself with different buffer sizes on different architectures.
A naive implementation of a minmax finder could look like below. It could of course also be templated to work with doubles or other data types without rewriting the code.
int clip_detection_custom_minmax(const AudioBuffer& buffer)
{
float min = std::numeric_limits<float>::max();
float max = std::numeric_limits<float>::min();
for (const auto& sample : buffer)
{
min = sample < min? sample : min;
max = sample > max? sample : max;
}
if (min < -1.0f || max > 1.0f)
{
return 1;
}
return 0;
}
From Rocket development board (gcc 8.1, 64 samples)
Looking at the numbers, it’s clear that std::minmax_elements isn’t nearly as fast as the naive implementation, which is almost 7 times faster. That’s unfortunate. Clearly we would prefer to use our custom implementation here. To better understand why it is so much slower, we need to look at the resulting assembly code. A really neat tool for that is Compiler Explorer. Full output here: https://godbolt.org/z/U-nglh. It’s not entirely obvious what is going on here. but we can see that there are no SIMD instructions used, and there are a number of branches in the code that could be detrimental to performance.
If we instead look at the assembly for our custom implementation above, which is much faster, (https://godbolt.org/z/Tk6Kh-) We see that not only has the compiler unrolled the loop into serial instructions, it has also implemented the comparisons with branchless SSE instructions that work on 4 floats at a time. It is also worth noting that the conditionals have been converted to branchless instructions by the compiler, which also should improve throughput.
...
minps xmm1, XMMWORD PTR [rax+48]
maxps xmm0, XMMWORD PTR [rax+48]
minps xmm1, XMMWORD PTR [rax+64]
maxps xmm0, XMMWORD PTR [rax+64]
...
Now if all we want is to detect some clipping, without caring about the amplitude of the clipped peaks, we could try a few options to make it even faster. One would be to return as soon as we find a value that is outside of the given range, and hence could clip if sent to an analog output.
int clip_detect_early_return(const AudioBuffer& buffer)
{
for (auto& sample : buffer)
{
if (sample > 1.0f || sample < -1.0f)
{
return 1;
}
}
return 0;
}
Another option would be to simply loop over the samples and count the number of potentially clipping samples. We’ll use std::abs here as well, to test for both positive and negative clipping at once.
int clip_detect_optimised(const AudioBuffer& buffer)
{
int clipcount = 0;
for (auto& sample : buffer)
{
clipcount += (std::abs(sample) > 1.0f);
}
return clipcount > 1;
}
We can clearly see that the early return function has very different performance depending on the amount of clipped samples in the buffer, this is not surprising as the function only needs to loop over a few samples to find a clipped sample if there are many of them, but if there are none, it has to loop over all the samples to find out. What it maybe not so obvious though, is that this also has a large impact on the worst-case performance. This is something we definitely want to avoid in a DSP algorithm. The second example, using std::abs() is, somewhat counter-intuitively, much faster, even though it always loops over all the samples in the buffer.
The key to the performance of the second version lies in the number of iterations being known at compile time, meaning that the compiler can both unroll the loop into one sequence of instructions, avoiding any costly branches, and parallelise the computation using SIMD instructions.
Using the gcc flag -fopt-info-vec-all we can have the compiler output a lot of information on the considerations it does when optimising. If we look at the output from gcc for the early return case, we see that the early return actually prevents gcc from vectorising the loop because the number of iterations is not fixed and cannot be determined during compilation.
...
<source>:70:16: note: === vect_analyze_loop_form ===
<source>:70:16: note: not vectorized: control flow in loop.
<source>:70:16: note: bad loop form.
...
Looking at the optimised case using std::abs below, we can clearly see that gcc analyses the loop, and calculates a minimum number of iterations where it would be worth vectorising it. It’s also worth noting that in this case std::abs is just as fast as using a custom abs function. And this is even slightly faster than our custom minmax algorithm above.
source>:83:25: note: Cost model analysis:
Vector inside of loop cost: 36
Vector prologue cost: 112
Vector epilogue cost: 123
Scalar iteration cost: 36
Scalar outside cost: 0
Vector outside cost: 235
prologue iterations: 2
epilogue iterations: 2
Calculated minimum iters for profitability: 8
<source>:83:25: note: Runtime profitability threshold = 8
<source>:83:25: note: Static estimate profitability threshold = 8
...
<source>:83:25: note: loop vectorized
Looking at the resulting assembly code (https://godbolt.org/z/yvN8Kt), we can see that gcc first implements “lead in” and “lead out” sections, where it handles the case where data is not aligned to SSE register boundaries. Then it does the bulk of the operation with SSE instructions, 4 floats at a time, loop unrolled, with the abs operation implemented using a branchless compare instruction. Exactly what we want for maximum performance:
...
movaps xmm3, XMMWORD PTR [rax+80]
psubd xmm0, xmm6
andps xmm3, xmm2
movaps xmm6, xmm1
cmpltps xmm5, xmm3
psubd xmm0, xmm7
movaps xmm3, XMMWORD PTR [rax+96]
movaps xmm7, xmm1
andps xmm3, xmm2
psubd xmm0, xmm4
cmpltps xmm6, xmm3
movaps xmm4, xmm1
...
So what about the exact opposite case? What if we do want to limit the audio to a certain range. Say when we are simulating an overdriven amplifier? Though hard clipping audio will probably sound a bit too harsh, for a nice, analogue sounding distortion, you would want something that saturates more gradually, like tanh() or a polynomial approximation of tanh, and not a hard clipper. But polynomial approximations are only valid within a certain range, so restricting values outside of that range would still make sense. C++17 introduced std::clamp which limits a value to a set range and seems like the perfect fit for this job. We could also write our own naive clip function like the one below, and compare that with the performance of std::clamp.
inline float float_clamp(float x, float min, float max)
{
if (x > max)
{
x = max;
}
if (x < min)
{
x = min;
}
return x;
}
And use it to process an AudioBuffer like
void custom_clamp(AudioBuffer& buffer)
{
for (auto& sample : buffer)
{
sample = float_clamp(sample, -1.0f, 1.0f);
}
}
Well, that was kind of disappointingly to see the naive implementation beat the standard library implementation again. But we could try a little trick of rewriting it using classic C/C++ notation with direct pointer access and not the modern range based way. I had previously seen that for older versions of gcc, using range based for-loops could restrict certain optimisation. So if we instead try the following, which should be equivalent.
void clamp_alg_direct_access(AudioBuffer& buffer)
{
for (unsigned int i = 0; i < buffer.size(); ++i)
{
buffer[i] = std::clamp(buffer[i], -1.0f, 1.0f);
}
}
We get these results:
And now we suddenly see the same performance as our previous, naive implementation. They even have the same assembly code (https://godbolt.org/z/CBbRdr), so clearly the compiler understood our intentions. So what is it that prevents the compiler from optimising the case using a range based for loop? In fact when we look at the implementation of std::clamp in the gcc standard library (below), it is not very different from our naive version above. It’s implemented using conditionals, but the logic is more or less the same. It takes arguments as references, though as it’s a small function in a header file, its likely to be inlined anyway.
template<typename _Tp>
constexpr const _Tp& clamp(const _Tp& __val,
const _Tp& __lo, const _Tp& __hi)
{
__glibcxx_assert(!(__hi < __lo));
return (__val < __lo) ? __lo : (__hi < __val) ? __hi : __val;
}
The full assembly of the function is short enough to be quite understandable even for someone like me, with a limited experience of assembly:
clamp_alg(std::array<float, 64ul>&):
movss xmm2, DWORD PTR .LC0[rip]
lea rax, [rdi+256]
movss xmm1, DWORD PTR .LC1[rip]
.L2:
movss xmm0, DWORD PTR [rdi]
add rdi, 4
minss xmm0, xmm2
maxss xmm0, xmm1
movss DWORD PTR [rdi-4], xmm0
cmp rax, rdi
jne .L2
ret
It does look like it is processing sample by sample and testing a branch every iteration. Apparently the compiler wasn’t able to vectorise the processing, or unroll the loop, things we’ve seen are crucial for performance. It even looks like it’s iterating over the data in reverse, which is a bit odd. The compiler output does give us a little bit of a clue though.
<source>:27:25: note: === vect_analyze_data_ref_accesses ===
<source>:27:25: note: not vectorized: complicated access pattern.
<source>:27:25: note: bad data access.
...
<source>:27:25: note: not consecutive access _6 = MEM[(const float &)__for_begin_18];
<source>:27:25: note: not consecutive access MEM[(float &)__for_begin_18] = prephitmp_3;
<source>:27:25: note: not vectorized: no grouped stores in basic block.
Using a range based for loop should give us a loop from the first element to the last, but it seems that the compiler is not able to figure this out . Even though the iterator from std::array should be a raw pointer to an element. it could be that this hides the underlying structure from gcc’s optimiser.
So far all the numbers shown has been with gcc 8.1. Will another compiler perform better or worse? We compiled the same code using clang 6 and got the results below. This is from the same Rocket development boards as the previous results:

We won’t go into much detail of the clang results for space reasons, but we can see that some things clang manages to optimise a bit more, like the custom minmax. Some things are a lot worse on the other hand, like the std::clamp, and the direct access trick doesn’t improve the results with clang.
You can download a repository with all the code used in this post from Github and try it out for yourself.
Should you use functions from std::algorithms in your audio processing code? The boring answer is “it depends”. As we’ve seen, in some cases it could be the best option and as performant as a custom implementation, in some cases it will perform significantly worse than an optimised algorithm. In particular if you’re writing your own vectorised functions.
A lot of the performance optimisations in audio processing comes from being able to parallelise and streamline using SIMD instructions, loop unrolling and similar techniques. The std::algorithm implementations are by nature very general and hence not natively vectorised in their implementations. How much the compiler can optimise depends on the extent it is able to figure out all access patterns and data structures. It appears function inlining is an absolute necessity for that to happen.
In the end the only solid advice we can give, is to profile your code and test each algorithm and it’s particular use case.
Found this interesting or still haven’t had all your questions answered? Please write us at tech@mindmusiclabs.com or leave a comment below.
[1] It’s easy to think that digital audio means dealing with discrete samples, when in fact we are dealing with a sampled representation of a continuous signal. And it is in fact possible for this continuous signal, reconstructed from discrete samples, to reach outside of [-1, 1] even though none of the discrete samples are outside this range. The reconstructed signal can then saturate the DAC or clip in the downstream analog circuitry. Detection of these intra-sample peaks is a much more complex problem that simply finding the minimum and maximum sample values. For a more in depth breakdown of the problem with intra-sample peaks, this article gives a good and detailed explanation: https://techblog.izotope.com/2015/08/24/true-peak-detection/